AdaMuon - Adaptive Muon Optimizer

1. Abstract

AdaMuon augments Muon with two mutually dependent modules:

1. a per-parameter second-moment (squared avg. of variance of gradients) modulation that captures orthogonal gradient updates to ensure update-level adaptivity
   • each parameter adapts its learning rate depending on how gradients vary in its own direction.
2. a RMS-aligned rescaling that regulates the overall update magnitude by aligning it with the intrinsic structure of the parameter space
   • instead of blindly clipping or normalizing, AdaMuon rescales updates so their RMS matches the intrinsic structure of the parameter space).

2. Preliminary

2.1 Muon Optimizer

• Refer to my blog on Muon up on my Notion site

1. Momentum update $M_t\leftarrow \beta M_{t-1}+G_t$​

• Purpose: accumulate gradient information over time (like SGD with momentum). $M_t$ keeps a smoothed history of recent gradients.
• Interpretation: $\beta$ controls how fast history decays. $\beta \approx 0.9$ means long memory; $\beta$ near $0$ means almost no momentum.

2. Compute orthogonal factor $O_t\leftarrow \text{Polar}(M_t,T,\epsilon )$

• Goal: instead of using $M_t$ (or a scalar-rescaled version) directly as the update direction, Muon extracts the orthogonal/polar component of $M_t$​.
• Why orthogonal? The polar factor captures the direction/rotation part of $M_t$​ (roughly the “direction” of the matrix, independent of singular values). This produces structured updates that respect parameter-space geometry (they are not purely per-coordinate scalings).
• How we compute it efficiently: full SVD of $M_t$ gives $M_t=U\Sigma V^{\top }$, and the orthogonal factor would be $U{V}^{\top }$. Full SVD is expensive, so Muon approximates $U{V}^{\top }$ by computing $O=M(M^{\top }M{)}^{-1/2}$ and approximating $(M^{\top }M{)}^{-1/2}$ with Newton–Schulz iterations.

3. Parameter update $W_{t+1}\leftarrow W_t-\eta O_t$

• We apply the orthogonal factor as the update direction, scaled by scalar learning rate $\eta$.
• This yields a structured step that preserves geometry (the orthogonal part gives a rotation-like or structure-preserving direction rather than per-coordinate scaling).

Variables:

• $W_t\in {\mathbb{R}}^{n\times m}$ — weight matrix at iteration $t$.
• $G_t\in {\mathbb{R}}^{n\times m}$ — gradient of the loss w.r.t. $W_t$​ at iteration $t$.
• $M_t\in {\mathbb{R}}^{n\times m}$ — momentum buffer at iteration $t$ (same shape as $W_t$​).
• $T\in {\mathbb{Z}}_{>0}$​ — number of Newton–Schulz iterations to approximate the polar factor (typical default $T=5$).
• $\Vert \cdot {\Vert }_F$​ — Frobenius norm.
• $I_k$​ — identity matrix of size k×kk\times kk×k.
• $O_t\in {\mathbb{R}}^{n\times m}$ — orthogonal/polar factor approximation for the momentum matrix $M_t$​ (same shape as $M_t$​).
• $\text{Polar}(A,T)$ — function that returns the polar (orthogonal) factor $O$ of matrix $A$ using $T$ Newton–Schulz iterations (detailed below).

2.2 Scaling up for Muon

• Muon - for 2D parameters (linear layers, weight matrices)
• Adam/AdamW - for 1D parameters (biases, layerNorm weights)
• Muon is scalable for LLM training, Liu et al. proposed to align the update scale of Muon with that of Adam, thereby allowing both optimizers to share a unified learning rate.

$${\gamma }_t=0.2\sqrt{\max (m,n)}$$ $${\mathbf{W}}_{t+1}={\mathbf{W}}_t-\eta \cdot ({\gamma }_t\cdot {\mathbf{O}}_t+\lambda {\mathbf{W}}_t)$$

• $\lambda$ — weight decay ratio
• $W_t\in {\mathbb{R}}^{n\times m}$
• This allows the optimizer to control the update RMS and also inherit the learning rate schedule of Adam, while still benefiting from Muon’s structured and geometry-preserving updates.

3. Algorithm

3.1 From Structured Updates to Variance-Aware Scaling

• Newton’s method uses curvature (via the Hessian Matrix or its inverse) to get locally optimal update directions. Full Hessian is too large for modern deep models so one uses approximations like the Fisher Information Matrix (FIM).
• Optimizers like Adam or RMSProp estimate gradient variance via exponential moving averages of squared gradients. This gives adaptive step sizes depending on how noisy the gradients are.
• Since Muon uses polar decomposition via Newton-Schulz iterations to get $O_t$, the identity

$$O_t=(M_t{M}_t^T{)}^{-1/2}{M}_t=M_t(M_t^T{M}_t{)}^{-1/2}$$

(explained in detail at The Polar Decomposition) captures second-order interactions across rows and columns, similarly to matrix-aware optimizers like Shampoo. But Muon doesn’t maintain full covariance or Hessian matrices. This is what gives Muon its row-/column-wise second-order sensitivity without computing full Hessian or full covariance matrices.

• While the orthogonal update captures global / matrix-level structure, it does not capture element-level gradient variance:

  • Some positions in the weight matrix may be extremely noisy (variance high), others very stable (variance low).
  • Uniform update magnitude (same scale for all entries) may cause:
    • Overshooting in high‐variance entries
    • Very slow/ineffective updates in low-variance entries

• Goal: keep the geometry-aware structure of Muon (via orthogonal updates), and add adaptivity at the element-level (fine-grained), like Adam does.

• Approach:

  1. Use Muon’s orthogonal direction $O_t$ as the base structured direction.
  2. Compute an element-wise second moment (variance estimate) over the entries of $O_t$.
  3. Use that variance estimate to modulate (scale) the entries of $O_t$​: downweight those with high variance (noisy), upweight or preserve those with low variance (stable).

• This modulation happens after orthogonal decomposition which ensures variance tracking happens on a “cleaned-up” version of the update direction (which has the large directional / global effects removed).

• Polar decomposition gives globally coherent, geometry-preserving update directions. Variance modulation gives adaptivity at coordinate level, better handling heterogeneity of gradient signals. Combined, they help avoid instabilities due to noise, allow faster learning in low-variance coordinates, while preserving structure.

3.2 Muon with Second-Moment Modulation

What is added on top of Muon

AdaMuon is an extension of the Muon optimizer, incorporating two extra mechanisms:

1. A second-moment estimator (operating element-wise, on the diagonal).
2. A norm-based global rescaling (to align the overall update magnitude, analogous to the RMS behavior in Adam).

• The core structured update of Muon (via polar decomposition/orthogonalization) is retained. AdaMuon does not replace this but augments it, making the update magnitude adaptive at the element level rather than uniform across all entries of the update matrix.

Equations & computation

1. Flatten the orthogonal update:

$$o_t=\text{vec}(O_t)$$

(Here, $O_t$ is flattened into a vector $o_t$.)

2. Second moment (variance) tracking, element-wise:

$$v_t={\beta }_2\cdot v_{t-1}+(1-{\beta }_2)\cdot o_t^2$$

where $o_t^2$ is the element-wise square, and ${\beta }_2$ is a decay parameter close to 1.

3. Bias correction:

$${\hat{v}}_t=\frac{v_t}{1-{\beta }_2^t}$$

This compensates for initialization bias since $v_0$ is typically initialized to zero.

4. Adaptive update direction: Define the adjusted vector via element-wise division:

$${\hat{o}}_t=\frac{o_t}{\sqrt{{\hat{v}}_t}+\epsilon }$$

where $\epsilon$ is a small constant for numerical stability.

5. Reshaping and global rescaling (RMS-aligned):

• Reshape ${\hat{o}}_t$ back to matrix form: ${\hat{O}}_t=\text{reshape}({\hat{o}}_t)$.
• Compute the RMS (root mean square) of ${\hat{O}}_t$: $\text{RMS}({\hat{O}}_t)$.
• Then, perform the final parameter update:

$$W_{t+1}=W_t-\eta \cdot \frac{0.2}{\text{RMS}({\hat{O}}_t)+\epsilon }\cdot {\hat{O}}_t+\lambda W_t$$

where:

• $\eta$ is the learning rate,
• $\lambda$ is the weight decay coefficient,
• $0.2$ is an empirically chosen constant scalar coefficient to align with Adam’s update scale.

Purpose & intuition

• Second-moment modulation: Allows AdaMuon to downweight coordinates with high noise (high variance) and upweight or preserve those that are stable (low variance). This helps prevent overshooting and instability in noisy directions.
• Global (RMS) rescaling: Ensures the overall magnitude of the update remains in a reasonable range, aligned with Adam’s scale. This provides consistency and allows for the reuse of standard learning rate schedules.
• Variance tracking post-orthogonalization: Ensures the update direction has already been geometrically “smoothed” (global structure normalized). This prevents element-wise adaptivity from undoing the benefits of the structural normalization.

Pseudocode

3.3 RMS-Aligned Rescaling

Purpose

• Ensure AdaMuon’s update magnitudes are compatible with learning-rate schedules designed for Adam (or Adam-style optimizers).
• Without this, the updates’ size can drift (get too small or too large), which breaks assumptions built into tuning schedules.

Key concept: dimension-aware target scale

• AdaMuon rescales its adaptive update so that the update’s norm (magnitude) matches a consistent target that depends on the parameter matrix dimensions.
• This uses matrix norms (Frobenius norm) and knowledge of dimensions $n$, $m$ of the weight matrix $W_t\in {\mathbb{R}}^{n\times m}$.

Equation & operations

Given:

• ${\hat{O}}_t$ = the matrix after variance-aware scaling and reshaping (same shape as original update).
• $\Vert {\hat{O}}_t{\Vert }_F$ = Frobenius norm of ${\hat{O}}_t$.
• $m,n$ = dimensions of weight matrix $W_t$.

Then:

1. Rescale ${\hat{O}}_t$ to enforce a Frobenius-norm based target norm:

$${\hat{O}}_t\leftarrow {\hat{O}}_t\cdot \frac{\sqrt{\min (n,m)}}{\Vert {\hat{O}}_t{\Vert }_F+\epsilon }$$

• (Here $\epsilon$ is a small constant for numerical stability.)
• Note: The paper sometimes writes $p\min (n,m)$ (contextually interpreted as $\sqrt{\min (n,m)}$).

2. Full parameter update (including weight decay and learning rate):

$$W_{t+1}=W_t-\eta \cdot \left({\gamma }_t\cdot \frac{\sqrt{\min (n,m)}}{\Vert {\hat{O}}_t{\Vert }_F+\epsilon }{\hat{O}}_t+\lambda W_t\right)$$

• Sometimes expressed equivalently as:

$$W_{t+1}=W_t-\eta \left(\frac{0.2}{\mathrm{RMS}({\hat{O}}_t)+\epsilon }{\hat{O}}_t+\lambda W_t\right)$$

Variables

• ${\hat{O}}_t$ — rescaled orthogonal update matrix (after second-moment modulation).
• $\Vert \cdot {\Vert }_F$ — Frobenius norm: $\Vert A{\Vert }_F=\sqrt{{\sum }_{i,j}{A}_{ij}^2}$.
• $n,m$ — dimensions of the weight matrix $W_t$.
• $\epsilon$ — small positive scalar for numerical stability.
• $\eta$ — learning rate.
• $\lambda$ — weight decay.
• ${\gamma }_t$ — scaling factor (often $0.2\sqrt{\max (m,n)}$ or similar) used earlier to align with Adam’s scale.

4. Experiment

4.1 Experimental Setup

1. Base Implementation
   • Framework: nanoGPT (Karpathy, 2022)
   • Architecture: GPT-2 (Radford et al., 2019)
   • Dataset: OpenWebText (Gokaslan et al., 2019)
2. Data Splits
   • Training set: ~9B tokens
   • Validation set: ~4.4M tokens
   • Tokenization: Standard GPT-2 tokenizer
3. Model Scales Evaluated
   • GPT-2 Small: 125M parameters
   • GPT-2 Medium: 355M parameters
   • GPT-2 Large: 770M parameters
   • GPT-2 XL: 1.5B parameters
4. Default nanoGPT Configurations
   • Bias terms: Removed from all linear layers
   • Activation function: GeLU
   • Dropout: 0.0 for all layers
5. Modifications Made
   1. Replace learned positional embeddings (WPE) with Rotary Positional Embedding (RoPE) (Su et al., 2024)
   2. Replace cosine learning rate schedule with Warmup-Stable-Decay (WSD) policy
6. Training Setup
   • Training tokens: ~50B tokens
   • Training steps: 100K steps
   • Warmup: 2K steps
   • Context length: 1024 tokens (for all models)

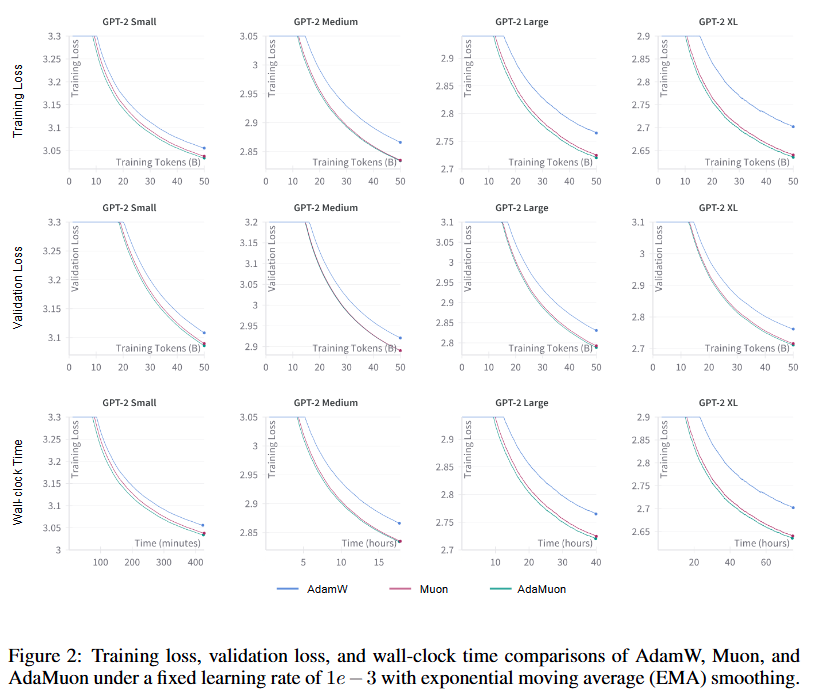
4.2 Result

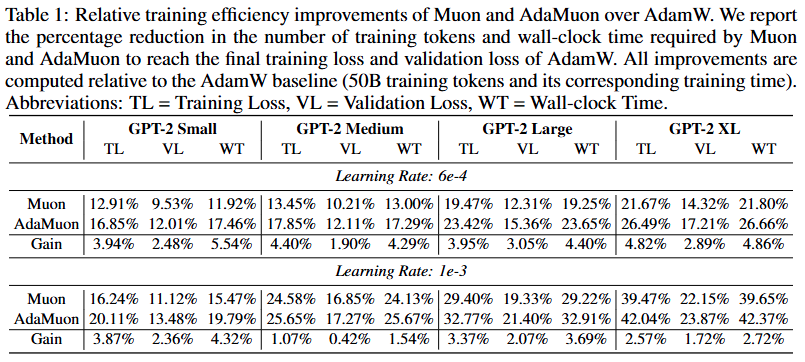
1. Efficiency Gains over AdamW
   • Both Muon and AdaMuon reduce the number of training tokens and wall-clock time needed to match AdamW’s final training and validation loss (at 50B tokens).
2. AdaMuon Superiority
   • AdaMuon consistently achieves the largest improvements across all model scales.
   • Shows faster convergence compared to both AdamW and Muon.
3. Convergence and Generalization
   • Figure below show that AdaMuon outperforms both baselines (AdamW and Muon) in:
     • Training loss reduction speed
     • Validation loss reduction speed
     • Generalization performance
4. Wall-Clock Cost
   • AdaMuon has a lower per-iteration wall-clock cost than Muon.
   • Its cost remains comparable to AdamW, despite additional mechanisms.
5. Overhead Analysis
   • Incorporating second-moment modulation and RMS-aligned rescaling adds negligible computational overhead.
   • These modifications lead to stabilized and more efficient optimization trajectories.

5. Conclusion

lr = $6e-4$

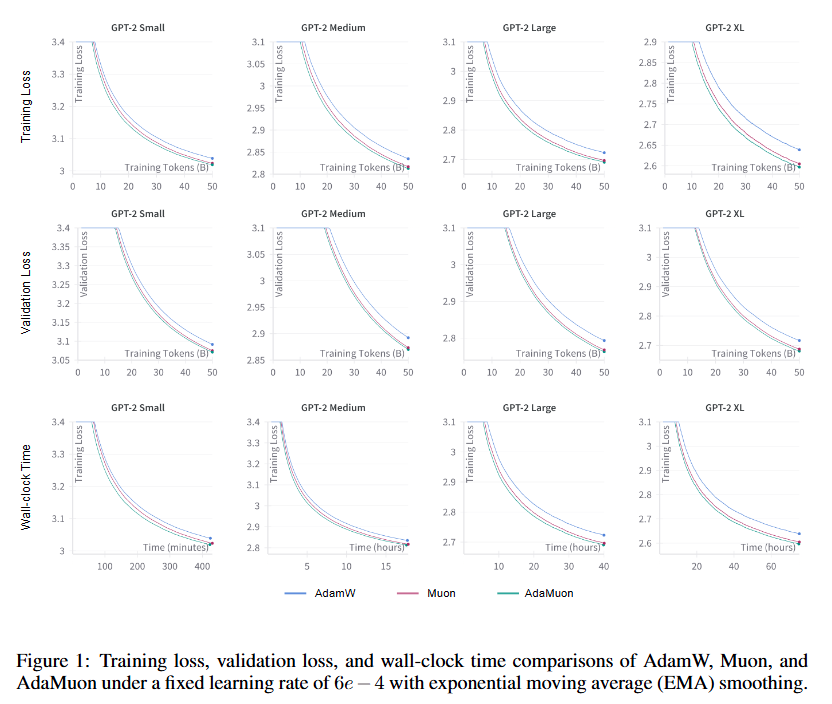
lr = $1e-3$